華德福數學教學分享—數學上可能的操作(下)
|
| 曾紫玉
|
|
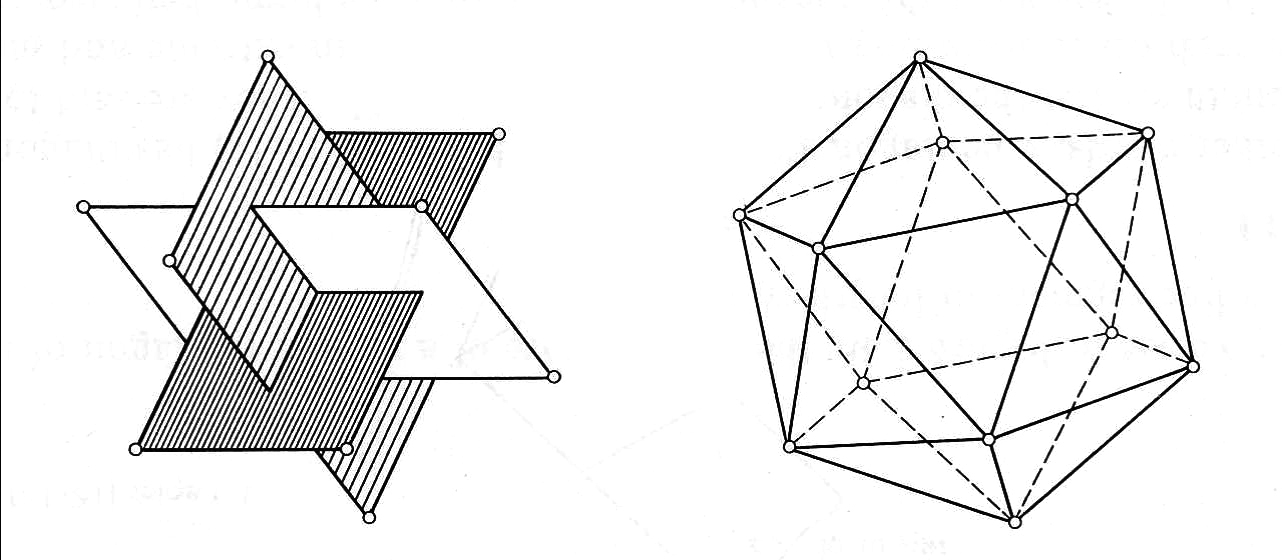
數學中的幾何課程一般很容易找到可以操作的部分,像是柏拉圖五種立體可以用多張摺紙互嵌來製作,或是用陶土塑形。其中一個很有意思的操作法是利用三張黃金矩形紙片互嵌,再讓學生想像每個頂點有線相連接時會變成甚麼形狀(這也是心靈肌肉運動之一,圖十一—二十面體)。我在網上看到國外的華德福學校,利用木棒兩端固定吸鐵,可以很方便地讓學生操作出這五種柏拉圖立體(註8)。
在非幾何的數學課中,我也希望可以讓學生有操作的部分,與圓相關的主題,我曾準備如明信片般大小的紙發給學生,問他們如何讓我可以從這麼小張紙中穿過?答案是有技巧地將紙剪成相連的一條線,展開如一個圓般,在他們學會如何簡易地剪開後,可以再挑戰學生用A4大小的紙張剪成一個大圓,讓全班都可以穿過去(註9)!主題是三角形時,也可以教學生製作六角翻
(Hexaflexagon),自己畫上各面的圖形,既好玩,又兼具藝術性(註10)。純思考會讓學生沉睡(吸入),手做則令學生醒過來(呼出),在華德福教學中很重視課程的節奏,老師得很有意識地讓睡和醒、呼和吸相互交織。
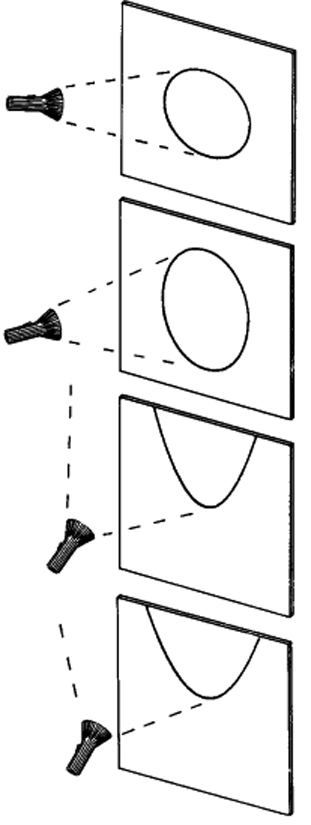
圓錐曲線除了作圖外,也有其他的操作方式。在學生都已經明瞭各曲線在圓錐中的分布位置後,一天早上我安排同學們站在一間實驗室走道的兩側,在全黑的室內,我用手電筒將光垂直打在走道上,並說:「歡迎來到圓錐王國!」慢慢地我轉換手電筒的角度,讓光圈從正圓形變成橢圓形,再繼續延伸光圈直到打到對邊牆上,我讓光圈來回移動的期間不斷地問學生:「你看到的是什麼曲線?」我自己備這門課時有幾個晚上都在玩手電筒,我不斷地問自己,這到底是橢圓的一端來到牆上,還是它是拋物線?我如何能區辨?最後我們回到教室講解:打出的光線一如圓錐,想像有個兩頭手電筒,那麼同時打出前後的光,就成了名符其實的圓錐王國,那麼地面就是之前切剖圓錐形陶土的剖面位置,至此,學生就能清楚分辨出:當燈光的邊緣與地面平行時,就是最關鍵的拋物線,光源往下就是橢圓,往上就是雙曲線(圖十二)。
另外,我會發下描圖紙,教學生如何輕易地摺出三種圓錐曲線(註11)。摺紙的部分操作起來相當容易,只要焦點與準線(或準圓)上的點一直重疊所摺出摺線就會形成圓錐曲線。這些操作簡單易行是以排在後頭,先苦後甘是必要的學習過程,否則已經會了簡單的作法再教難的作圖,那麼老師就是拿磚頭砸自己的腳了。
天大的祕密
圓錐國王很高興王子這麼優秀,竟然還可以用手電筒和摺紙解開寶藏埋藏之所在,於是積極地籌備王子與公主的婚禮,也吐出圓錐王國的天大祕密-曲線的形變。
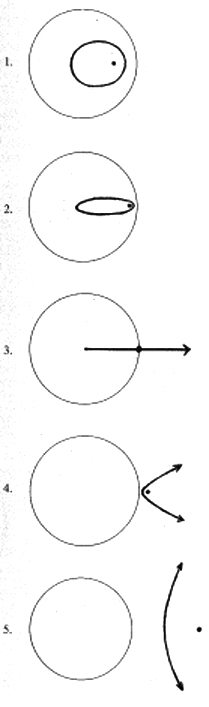
這就進到圓錐曲線的壓軸好戲。第一個形變的秘密比較簡單:此時學生已明瞭當焦點在準圓內外不同距離時曲線的形變,但是問題是—如果焦點就正好在準圓上時,曲線會變成啥樣呢?學生可從作圖中自己找出答案(圖十三之3-為一射線)。
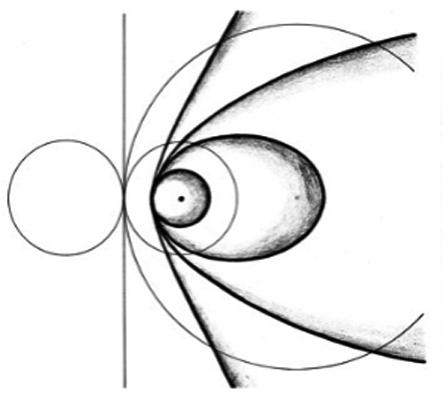
秘密之二(圖十四)最難理解:當一個圓的最右側這一點不動,而圓心往左邊移動時,圓會變大,圓和焦點(位於圓右側)等距的軌跡就形成雙曲線;當圓心一直往左移動,圓變得越來越大,是以雙曲線的開口就越來越小,圓心最後到了左邊無窮遠那點時,黑板上的圓大到只看得到它的一小部分,而且看起來就像一條直線,這條直線和右側的焦點等距的軌跡就變成拋物線;當圓心過了無窮遠這一點時,圓心到哪裡去了?學生在七年級的物理課(凸透鏡成像作圖)中已經先有體驗(實像變大到後來不見了,而轉成虛像從另一側出現),是以有學生可以猜到答案-圓心過了左側無窮遠後是從右側的無窮遠處回來。而在圓的最右側這一點仍不動的情況下,圓心在右,是以焦點變成在圓內,焦點與圓等距的軌跡變成超扁長的橢圓曲線;當圓心繼續往左移動,橢圓變得越來越圓胖;等圓心與焦點重合時,橢圓就變成正圓了。
這真是令人不可思議的形變,所有的圓錐曲線互相變來變去,就好像都是同一條!這點與我們在天文上的發現有異曲同工之妙:地球繞行太陽的軌跡為橢圓形,太陽位於橢圓的一個焦點上,當太陽系行星運行速度增大到某種程度,它們就會沿拋物線或雙曲線運行,而人類發射人造地球衛星時就要遵照這個原理。
數學的規律美、驚嘆、巧合等例子俯拾皆是,應該要適時地帶給孩子。我很喜歡一個有關圓周長、很酷的例子,在圓的主題結束前問了同學:假設有一條很長的繩子(假設四萬公里),恰恰好沿赤道繞地球一周,然後我們把繩子加長一公尺,請問一隻老鼠可以鑽得過這個鬆動的地球腰帶嗎?如果你動一動筆算看看的話,會發現連一隻貓都可以鑽得過去喲!這種經過計算可以確實得到超乎原本想像的答案,就是成人也會驚異,學生在當中就更能感受到掌握數學的絕妙。
晨圈
主課程的一開始是晨圈活動,我們玩拋沙包,每天距離越拉越遠、籃子也越換越小,總要一直挑戰學生,最後一天懸掛一個鈴鐺在半空,附近放個大口鍋子,要沙包打到鈴鐺掉入鍋中才算數。這個拋物(線)練習,雖然只是用身體來體驗控制拋物線,但是深受學生歡迎,而一些數學能力不好的同學這時很可能反而會被注目(投進率超高),適時地讓不同的學生有機會秀出其亮眼之處,也是我的目的之一。
晨圈除了拋沙包之外,隨著課程的進展,我讓學生直接用身體來體驗這些曲線,把人當成焦點,一排人變成準線(或準圓),給條繩作為測量工具,讓學生自己安排其他的學生站在等距軌跡的位置,方法都對了,還可以玩形變,但不會一直重複相同的事。教橢圓時,我帶了一次很特別的晨圈,由於當天會講到「克卜勒第二運動定理」
(地球走在繞行太陽的橢圓形軌道時,靠近太陽時運行的速度較快,遠離太陽時速度較慢),我帶學生一起體驗「承氣」的動作(註12),學生可以感受到雙手揮動時所畫出的橢圓,在靠近身體的時候手動得快,離身體遠的時候手就動得慢。等課程中要說明克卜勒的發現時,讓學生回想晨圈做的動作,就似乎更容易連結。事實上每個人的身體就是個小宇宙。
您也許要問為何物理素材進到數學課中,史丹勒要我們在課程中靈活地教學,在不失去科目、不帶領學生偏離主題的情況下,通過將科目交織在一起,而跟人產生關聯。另外,哥德也說:「人就是宇宙自然的縮小版,所有的自然現象都可以在人身上發現。」特別是史丹勒要老師們在孩子過了九或十歲(跨越盧比孔河階段)後,課程必須始終將人類與其他的自然界互做比較,並希望老師可以帶給孩子一種「人與整個自然界相似」的感受。(註7)
點心故事
猶記資深外師 Loather 給了我們一個數學主課程的圖像,他提到三個最基本的元素:晨圈、進新內容前的回顧,和一個十五分鐘的甜點故事做為結束。剛開始時,我一直覺得講故事這一點窒礙難行,除了貪心想多上些正課,通常教第一輪的華德福老師光是準備課程內容就很累了,哪裡有力氣去另外張羅故事?我跟
Loather 討價還價,問能不能講十分鐘的故事就好?外師堅定地回答我說要十五分鐘,原因是太短的故事營造不出感受。然而這甜點故事並不要求搭配數學主課程的內容,反而是配合不同年級孩子的需求而定;它不需要像歷史主課程一樣得用「說」的,而是可以拿著書「讀」給孩子們聽。一位同事對她的班級年齡適合且喜歡讀的書瞭若指掌,每天在數學主課的末尾時讀一段,等講到最精彩的部分戛然而止,又開始讀另一本。被吊起胃口的學生則爭相借書回去讀,這樣下來,充滿思考與意志的數學主課也能兼顧滋養情感面,達到所謂「甜點」的效果,也啟動了孩子的閱讀興趣,真是一舉兩得。
我自己能真的實踐在數學主課程每天講甜點故事已是幾年之後的事了,也的確感受到外師所說的「對孩子的滋養」。記得在結束「圓」面積課程的那一天,我講了一個圓的故事—失落的一角
(The missing part)。其中描寫一個圓缺了一角,他出發去尋找那能圓滿他缺憾的一角的種種經歷,故事簡單,但發人深省。網上可以看到已經有前輩們將故事製成投影片,可以很方便地放給學生看;但是我很享受一頁頁(印成A3大小的黑白畫)講給學生聽的過程,孩子眼睛看的是單純的黑白線條,聽的是人的聲音,可緩、可急、可營造張力,學生完全地融入故事當中。這次的圓錐曲線主課程,我一天講一位現代人物特寫。在華德福教育中很推薦國中生看人物傳記,因為這個時期的他們需要找尋人生典範。從他們專注的聆聽表情中,我可以看到有些種子被深埋在他們的心中,也許因緣際會的一天就發出芽來。對聽數學只有乏味可言的少數學生而言,這堂課總還算有一些收穫或娛樂。
當然,這個主課程的最後結局就是王子娶到美麗的公主。為了將課程設計成尋寶的故事,我邊教邊想辦法將隔天的內容納入故事的流中,可以這樣天馬行空地串聯,自己還頗樂在其中,於是再次教圓錐曲線主課時,我讓學生可以自編故事,工作本除了是學習的累積,也成了自我創作的園地。
結語:
即便如此,我還是要提醒老師們揚棄所謂的華德福的框架。前面所提到的甜點故事、晨圈等等,並非一個固定、僵化的必要內容,反而應回歸到華德福教育中所強調的本質-
如何在一個課程中同時兼顧思考、情感和意志三者。同樣是一門三周的圓錐曲線主課程,每位老師都可以有自己的規劃與設計,這裡只是略拋一磚而已。
我要藉此機會感激一開始就遇到的德籍啟蒙恩師 Loather Steinmann,他一路陪伴在台灣新設立的華德福學校,我也在他的指導下過了最初、最煎熬的三年華德福導師生涯。Loather
除了給予我們許多教學實務上的指導、人智學的理念,也為我們打破許多「所謂華德福」的框架,同時給予我們不怕犯錯的勇氣與信心。我今天能摸到一點華德福的門檻,能有一點點的教學成效,都要歸功於他。雖然
Loather 在前年六月與世長辭,但他堅定、溫暖、風趣,又帶著智慧的言行風範,仍然在我心深處提攜著我往前邁進,謝謝您,Loather。
註1:
”Making Math Meaningful: A Source Book for Teaching
Middle School Math”, by Jamie York, Bob & Nancy's Services, Inc.
註2:
”Geometry and the Imagination-The Imaginative Treatment
of Geometry in Waldorf Education”, A. Renwick Sheen, Waldorf Publications.
註3:
「青少年教育」第一講,魯道夫‧史丹勒著,呂丹、孫愛萍譯,華德福生活館出版。
註4:
我之所以會在冥想前安排得這麼複雜,是因為一旦你直接要學生閉上眼睛,很多人就順勢趴下,睡大頭覺去了。
註5:
橢圓上任一點到兩焦點的距離和為一定值,是以為加法的曲線;雙曲線上任一點到兩焦點的距離差唯一定值,是以為減法的曲獻;拋物線原本的定義就是到焦點和到準線的距離相等,是以為相等的曲線。
註6:
找一條拉鍊,拉開一部分,在拉開的兩邊各選擇一點F1和F2,使它們到拉開P點的長度不相等。在P點處放上一支鉛筆,逐漸拉開拉鍊,鉛筆跟著移動,這樣就畫出一條曲線。摘自「幾何的寶藏」,作者李毓佩,國家圖書館出版社。
註7:
「實用教學指引—華德福學校1~8年級課程的圖像」,魯道夫.施泰納著,林琦珊譯,洪業文化出版。
註8:
參考網站:Eighth Grade Platonic Solids Project,https://www.youtube.com/watch?v=rWrKMeS-Vio
註9:
「如何穿過一張明信片—德國小學生愛上數學的祕密」,波伊特許帕赫博士、馬庫斯.華格納合著,譯者:姬健梅,究竟出版社。
註10:
參考網站:How to Make Tri Hexaflexagon Tutorial Out of a Paper – DIY Tri Hexaflexagon,https://www.youtube.com/watch?v=9iDEqX5eAr8
註11:
參考網站:Conics – Making a Hyperbola with Wax Paper,https://www.youtube.com/watch?v=nEISCCjObPg,另外兩種曲線的摺法,由此很容易連結到。
註12:
「承氣」動作:尾椎有如對著一正方形地墊的頂點,兩大腿外側貼平於正方形的兩邊(呈九十度角),兩腳掌面相對貼好(如膝蓋不好的人,則需墊高臀部),脊椎打直,兩手懸於大腿之上,掌面攤平朝上。開始動作時,脊椎前傾十五度,兩手朝前往內繞回畫圓,兩手不相碰,指尖維持朝前,可依自己的速度,接近身體但不碰到身體,如此畫出的圓為橢圓形,而靠近身體時速度較快畫出,遠離身體時速度變慢收回。要停下來時,則將脊椎當排檔桿煞車,回到脊椎打直的狀態,手的動作就會慢慢停下來了(源自「無相氣學」功法之一)。
圖十一:黃金矩形與二十面體
圖十二:
手電筒製造圓錐曲線
圖十三:秘密之一
圖十四:秘密之二
後記—華德福幾何課程樣貌:
從人智學人的發展論中,十二歲以後邏輯思維才開始萌芽,是以此時才開始用適當的方法帶進幾何,使其與內在產生真實的連結。除此之外,還要教授帶有想像力品質的幾何。
華德福教育在國小階段上形線畫與優律思美,這時用身體帶入了幾何的形;五年級上徒手幾何,六年級上尺規作圖,帶入工具(圓規)的應用,七年級驗證畢氏定理並且學習透視
(Perspective),讓學生從二度的平面空間裡生出三度空間,八年級上柏拉圖立體幾何時,更能在心中看到正多面體的結構與互相內嵌(對偶性),接著才進入圓錐曲線。
圓錐曲線基本上是同一曲線在不同階段形變後的結果,亦是了解宇宙、地球、人的形的基礎,這點到十一年級的投影幾何(Projective Geometry) 主課程會有更深化的感受。圓錐曲線這門主課程透過繪圖的經驗,得以刺激孩子的想像力(這是數學發明的推動力),讓孩子能清楚地定義這些曲線的軌跡,並看到不同條件下的形變,且能為日後更為抽象與智識的訓練奠下一堅實的基礎。
|
 本期目錄
本期目錄 上篇文章
上篇文章 下篇文章
下篇文章 本期目錄
本期目錄 上篇文章
上篇文章 下篇文章
下篇文章 本期目錄
本期目錄 上篇文章
上篇文章 下篇文章
下篇文章